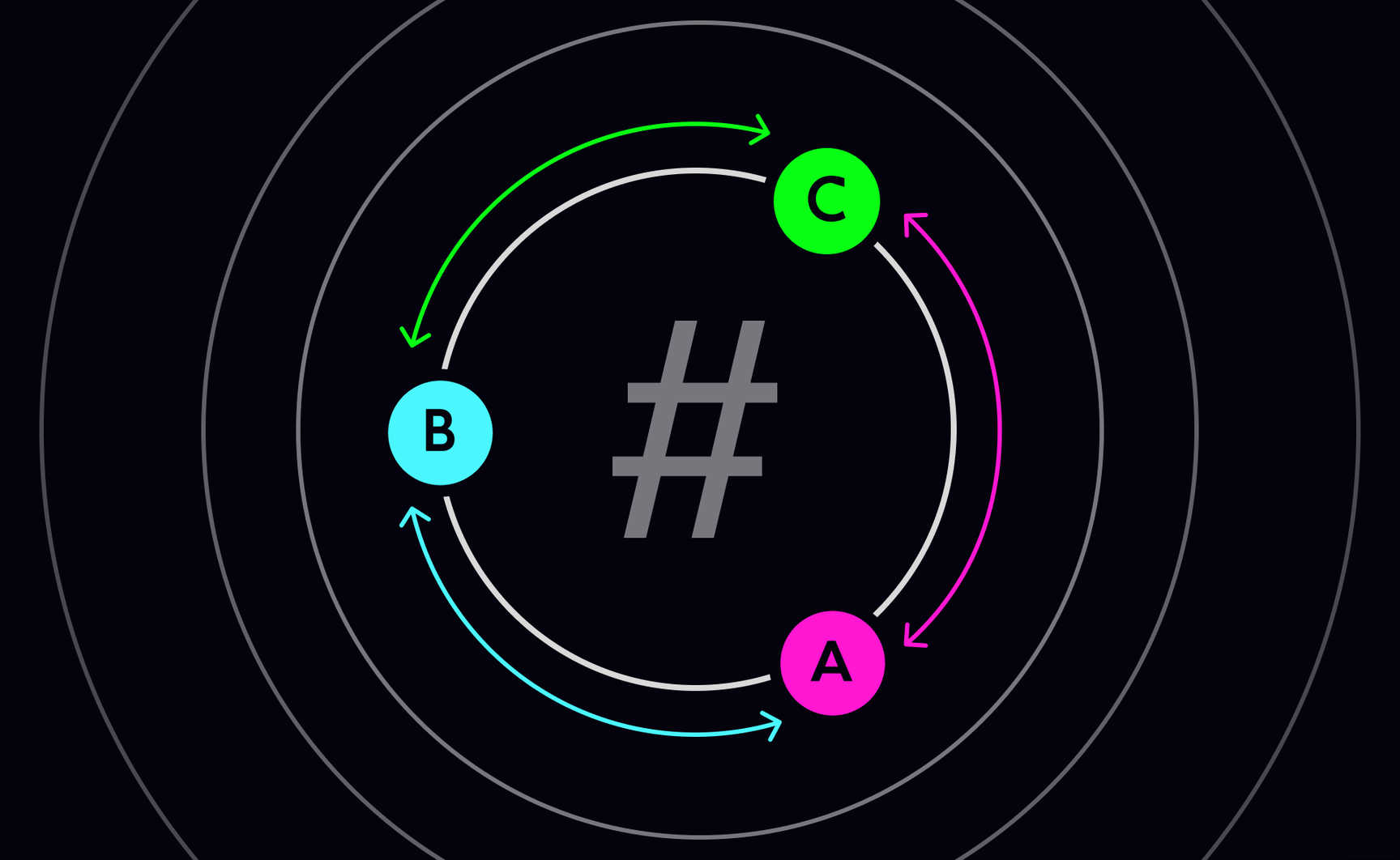
Consistent hashing explained

Consistent hashing is used in distributed systems to keep the hash table independent of the number of servers available to minimize key relocation when changes of scale occur.

In this article, I explain consistent hashing: what it is and why it is an essential tool in scalable distributed systems.

I’ll look at data structures to implement a consistent hashing algorithm efficiently at scale. Finally, I introduce a working example of a consistent hashing implementation.

Here is a summary of what I will cover:

• What is hashing?
• Hashing in a distributed system
• What is consistent hashing?
• How does consistent hashing work?
• How to implement a consistent hashing algorithm
• An example of consistent hashing
• Consistent hashing optimization
• Consistent hashing FAQs

What is hashing?

The classic hashing approach uses a hash function to generate a pseudo-random number, which is then divided by the size of the memory space to transform the random identifier into a position within the available space. Something that looks like the following:

Why use hashing?

Using a hash function ensures that resources required by computer programs are efficiently stored in memory, and that in-memory data structures are loaded evenly to make information retrieval more efficient.

Hashing in a distributed system

In a scenario where various programs, computers, or users request resources from multiple server nodes, we need a mechanism to map requests evenly to available server nodes, thus ensuring that the load is balanced for consistent performance.

In the classic hashing method, we always assume that:

• The number of memory locations is known, and
• This number never changes.

It’s common for a cluster to scale up and down, and there are always unexpected failures in a distributed system. We cannot guarantee that the number of server nodes will remain the same. What if one of them fails? With a naive hashing approach, we need to rehash every single key as the new mapping is dependent on the number of nodes and memory locations, as shown below:

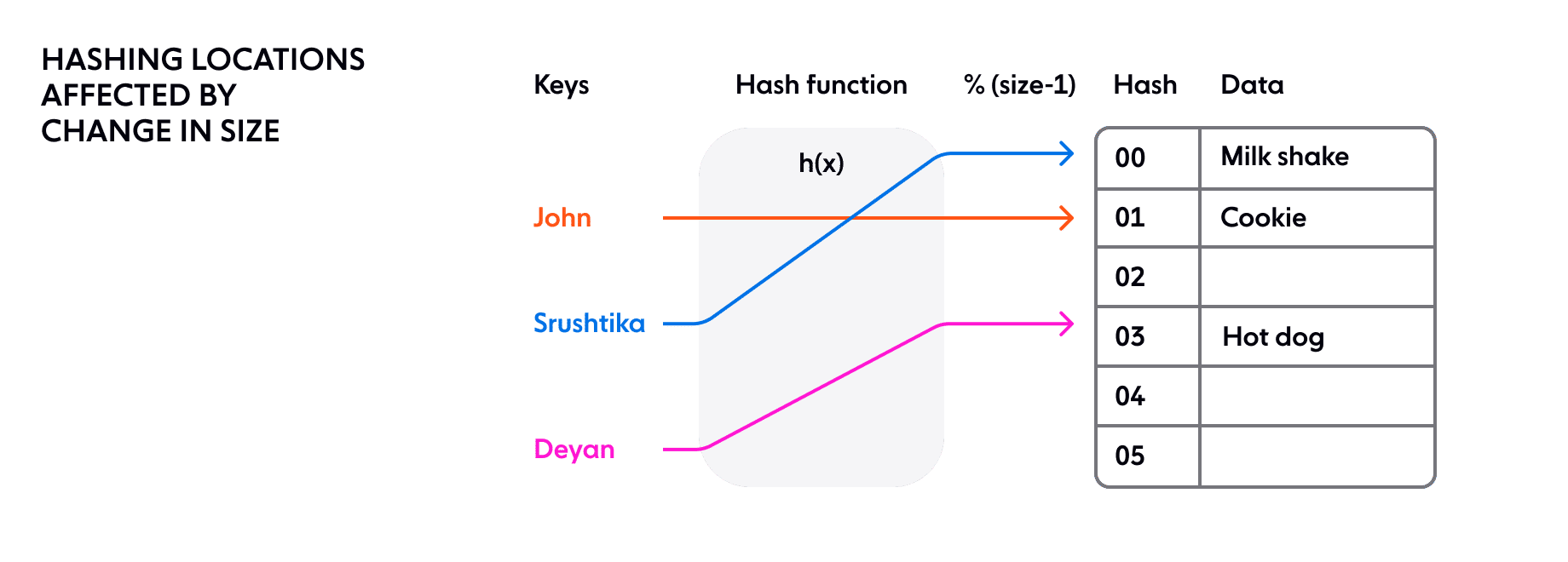
The problem in a distributed system with simple rehashing —moving the placement of every key — is that state is stored on each node. A small change in the cluster size could result in a reshuffle of all the data in the cluster. As the cluster size grows, this becomes unsustainable because the amount of work required for each hash change grows linearly with cluster size.

This is where the concept of consistent hashing comes in.

What is consistent hashing?

Consistent hashing can be described as follows:

• It represents the resource requestors (which I shall refer to as ‘requests’) and the server nodes in a virtual ring structure known as a hashring.
• The number of locations is no longer fixed, but the ring is considered to have an infinite number of points, and the server nodes can be placed at random locations on this ring. (Of course, choosing this random number again can be done using a hash function, but the second step of dividing it by the number of available locations is skipped as it is no longer a finite number).
• The requests, that is, the users, computers or serverless programs, which are analogous to keys in the classic hashing approach, are also placed on the same ring using the same hash function.

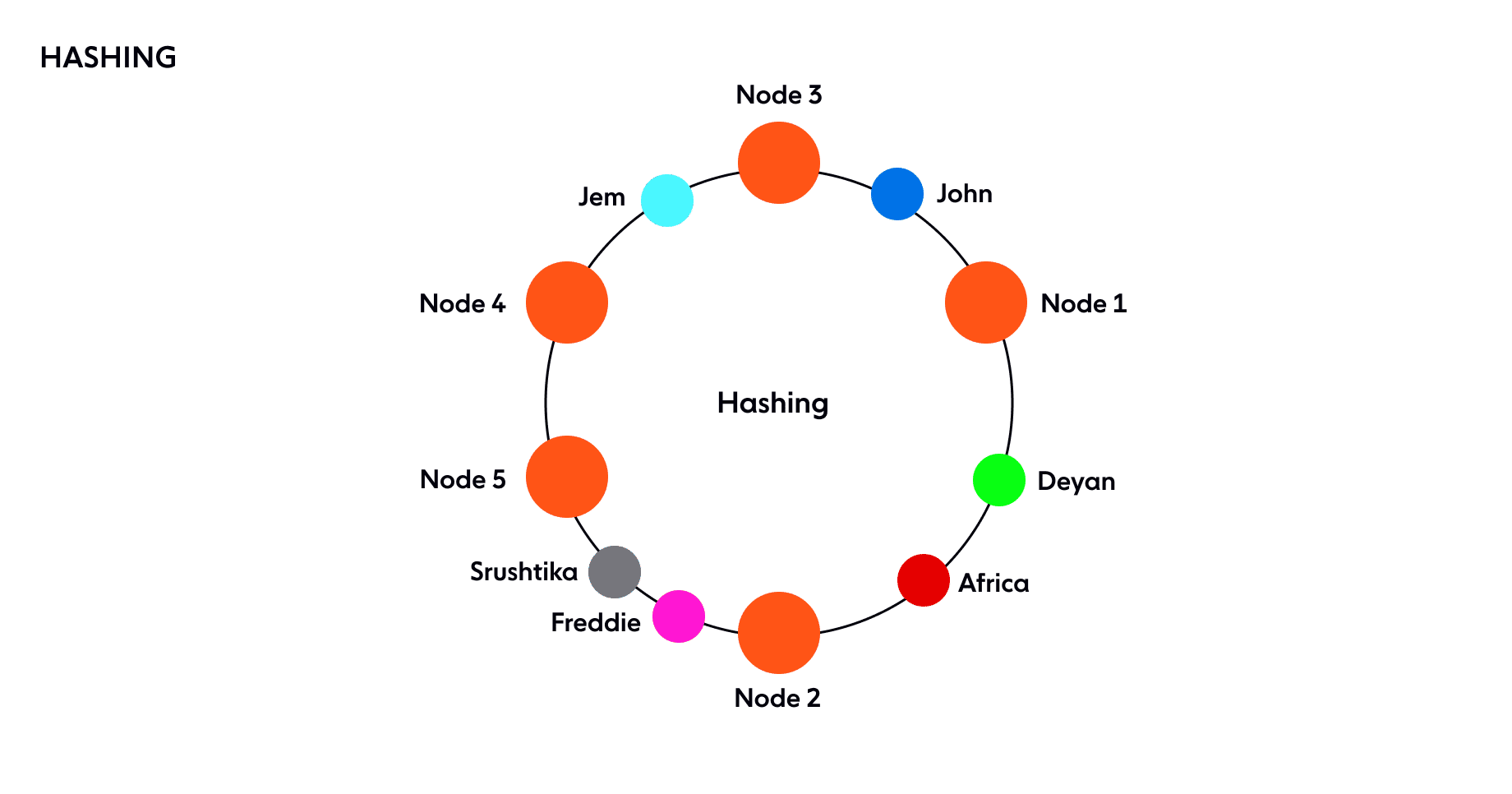
How is the decision about which request will be served by which server node made? If we assume the ring is ordered so that clockwise traversal of the ring corresponds to increasing order of location addresses, each request can be served by the server node that first appears in this clockwise traversal.

That is, the first server node with an address greater than that of the request gets to serve it. If the address of the request is higher than the highest addressed node, it is served by the server node with the lowest address, as the traversal through the ring goes in a circle (illustrated below):

Theoretically, each server node ‘owns’ a range of the hashring, and any requests coming in at this range will be served by the same server node.

How does consistent hashing work?

Now, what if one of these server nodes fails, say Node 3, the range of the next server node widens and any request coming in all of this range, goes to the new server node.

But that’s it. It’s just this one range, corresponding to the failed server node, that needed to be re-assigned, while the rest of the hashring and request-node assignments still remain unaffected.

Contrast this with the classic hashing technique in which a change in size of the hash table effectively disturbs ALL of the mappings. Thanks to consistent hashing, only a portion (relative to the ring distribution factor) of the requests will be affected by a given ring change. (A ring change occurs due to an addition or removal of a node causing some of the request-node mappings to change.)

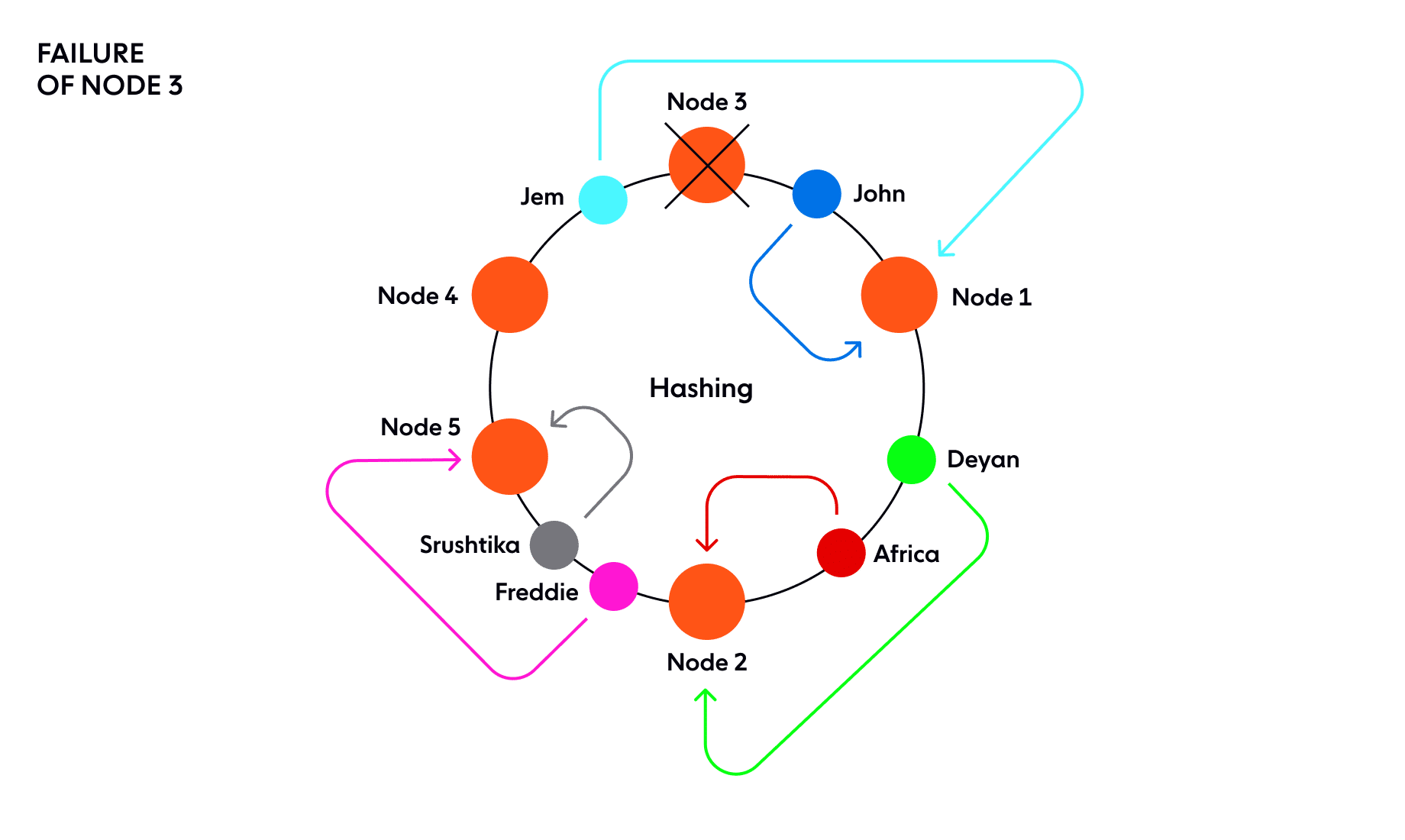
How to implement a consistent hashing algorithm

Now that we’re comfortable with what a hash ring is, we need to implement a mapping from our hash space to nodes in the cluster to find the nodes responsible for a given request.

We need a hash function to compute the position in the ring given an identifier for requests. We also need a way to determine which node corresponds to a hashed request. For this, we can use a simple data structure that comprises the following:

• An array of hashes that correspond to nodes in the ring.
• A map (hash table) for finding the node corresponding to a particular request.

This is essentially a primitive representation of an ordered map.

To find a node responsible for a given hash in the above structure, we need to:

• Perform a modified binary search to find the first node-hash in the array that is equal to or greater than (≥) the hash you wish to look up.
• Look up the node corresponding to the found node-hash in the map

Addition or removal of a node

As I explained at the beginning of the article, when a new node is added, some portion of the hashring, comprising of various requests, must be assigned to that node. Conversely, when a node is removed, the requests that had been assigned to that node will need to be handled by some other node.

How to manage a ring change

One solution is to iterate through all the requests allocated to a node. For each request, we decide whether it falls within the bounds of the ring change that has occurred, and move it elsewhere if necessary.

However, the work required to do this increases as the number of requests allocated to a given node scales. The number of ring changes tends to increase as the number of nodes increases. In the worst case, since ring changes are often related to localized failures, the load associated with a ring change could increase the likelihood of other affected nodes as well, possibly leading to cascading issues across the system.

To counter this, and make relocation of requests as efficient as possible, we store all requests in a data structure that allows us to find those affected by a single hash change anywhere on the ring

How to find affected hashes

Adding or removing a node from the cluster will change the allocation of requests in some portion of the ring, which we will refer to as the affected range. If we know the bounds of the affected range, we will be able to move the requests to their correct location.

To find the bounds of the affected range, starting at the hash H of the added or removed node, we can move backwards (counter-clockwise in the diagram) around the ring from H until another node is found. Let’s call the hash of this node S (for start). The requests that are anti-clockwise from this node will be located to it, so they won’t be affected.

Note that this is a simplified depiction of what happens. In practice,  we use replication factors of greater than 1, and specialized replication strategies in which only a subset of nodes is applicable to any given request.

The requests that have placement hashes in the range between the found node and the node that was added (or removed) are those that need to be moved.

How to find the affected range of requests

One solution is simply to iterate through all the requests corresponding to a node, and update the ones that have a hash within the range.

In JavaScript that might look something like this:

for (const request of requests) {
  if (contains(S, H, request.hash)) {
    /* the request is affected by the change */
    request.relocate();
  }
}

function contains(lowerBound, upperBound, hash) {
  const wrapsOver = upperBound < lowerBound;
  const aboveLower = hash >= lowerBound;
  const belowUpper = upperBound >= hash;
  if (wrapsOver) {
    return aboveLower || belowUpper;
  } else {
    return aboveLower && belowUpper;
  }
}

Since the ring is circular, it is not enough to just find requests where S <= r < H, since S may be greater than H (meaning that the range wraps over the top of the ring). The function contains() handles that case.

Iterating through all the requests on a given node is fine as long as the number of requests is relatively low or if the addition or removal of nodes is relatively rare.

However, the work required increases as the number of requests at a given node grows. Worse still, ring changes tend to occur more frequently as the number of nodes increases, whether due to automated scaling or failover, and this can generate load across the system to rebalance the requests. It may even increase the likelihood of failures on other nodes, possibly leading to cascading issues across the system.

To mitigate this, we also store requests in a separate ring data structure similar to the one discussed earlier. In this ring, a hash maps directly to the request that is located at that hash.

Then we can locate the requests within a range by doing the following:

• Locate the first request following the start of the range, S.
• Iterate clockwise until you find a request that has a hash outside the range.
• Relocate those requests that were inside the range.

The number of requests that need to be iterated for a given hash update will on average be R/N where R is the number of requests located in the range of the node and N is the number of hashes in the ring, assuming an even distribution of requests.

An example of consistent hashing

Let’s put the above explanation into action with a working example:

Suppose that we have a cluster containing two nodes A and B.

Let’s randomly generate a ‘placement hash’ for each of these nodes: (assuming 32-bit hashes), so we get

• A: 0x5e6058e5
• B: 0xa2d65c0

This places the nodes on an imaginary ring where the numbers 0x0, 0x1, 0x2… are placed consecutively up to 0xffffffff, then returns through the circle to be followed by 0x0.

Since node A has the hash 0x5e6058e5, it is responsible for any request that hashes into the range 0xa2d65c0+1 up to 0xffffffff and from 0x0 up to 0x5e6058e5, as shown below:

B on the other hand is responsible for the range0x5e6058e5+1up to 0xa2d65c0. Thus, the entire hash space is distributed.

This mapping from nodes to their hashes needs to be shared with the whole cluster so that the result of ring calculation is always the same. Thus, any node that requires a particular request can determine where it lives

Say we want to find (or create) a request that has the identifier ‘[email protected]’.

1. We compute a hash H of the identifier, say 0x89e04a0a
2. We look at the ring and find the first node with a hash that is greater than H. Here that happens to be B.

Therefore B is the node responsible for that request. If we need the request again, we will repeat the above steps and land again on the same node, which has the state we need.

This example is a bit oversimplified. In reality, having a single hash for each node is likely to distribute the load quite unfairly. As you may have noticed, in this example, B is responsible for (0xa2d656c0-0x5e6058e5)/232 = 26.7% of the ring, while A is responsible for the rest. Ideally, each node would be responsible for an equal portion of the ring.

Consistent hashing optimization

One way to improve the approach is to generate multiple random hashes for each node, as below:

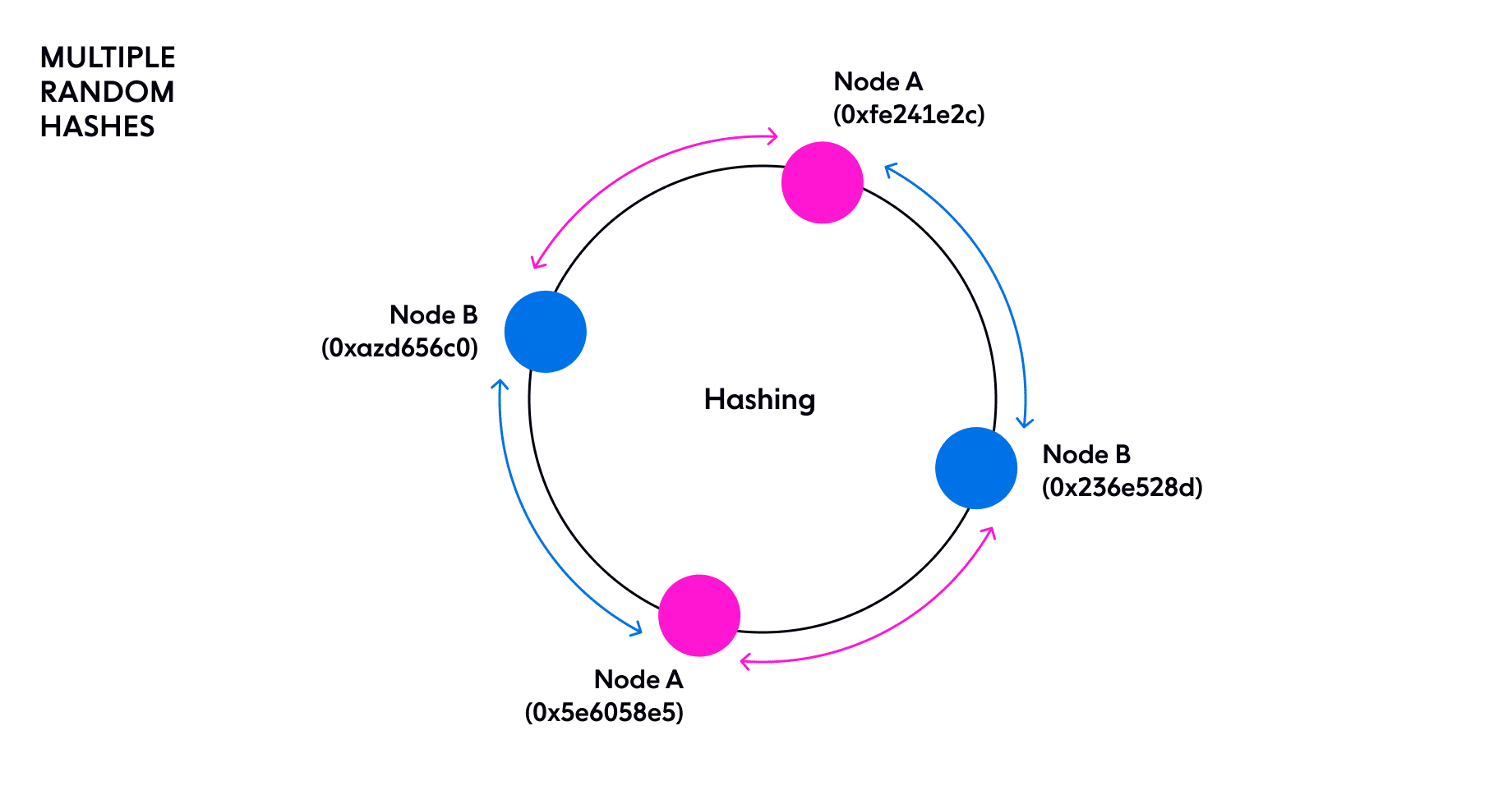
In reality, we find the results of this are still unsatisfactory, so we divide the ring into 64 equally sized segments and ensure a hash for each node is placed somewhere in each segment. The aim is just to ensure each node is responsible for an equal portion of the ring, so that load is evenly distributed. (Another advantage of having multiple hashes for each node is that the hashes can be added to or removed from the ring gradually to avoid sudden spikes of load. )

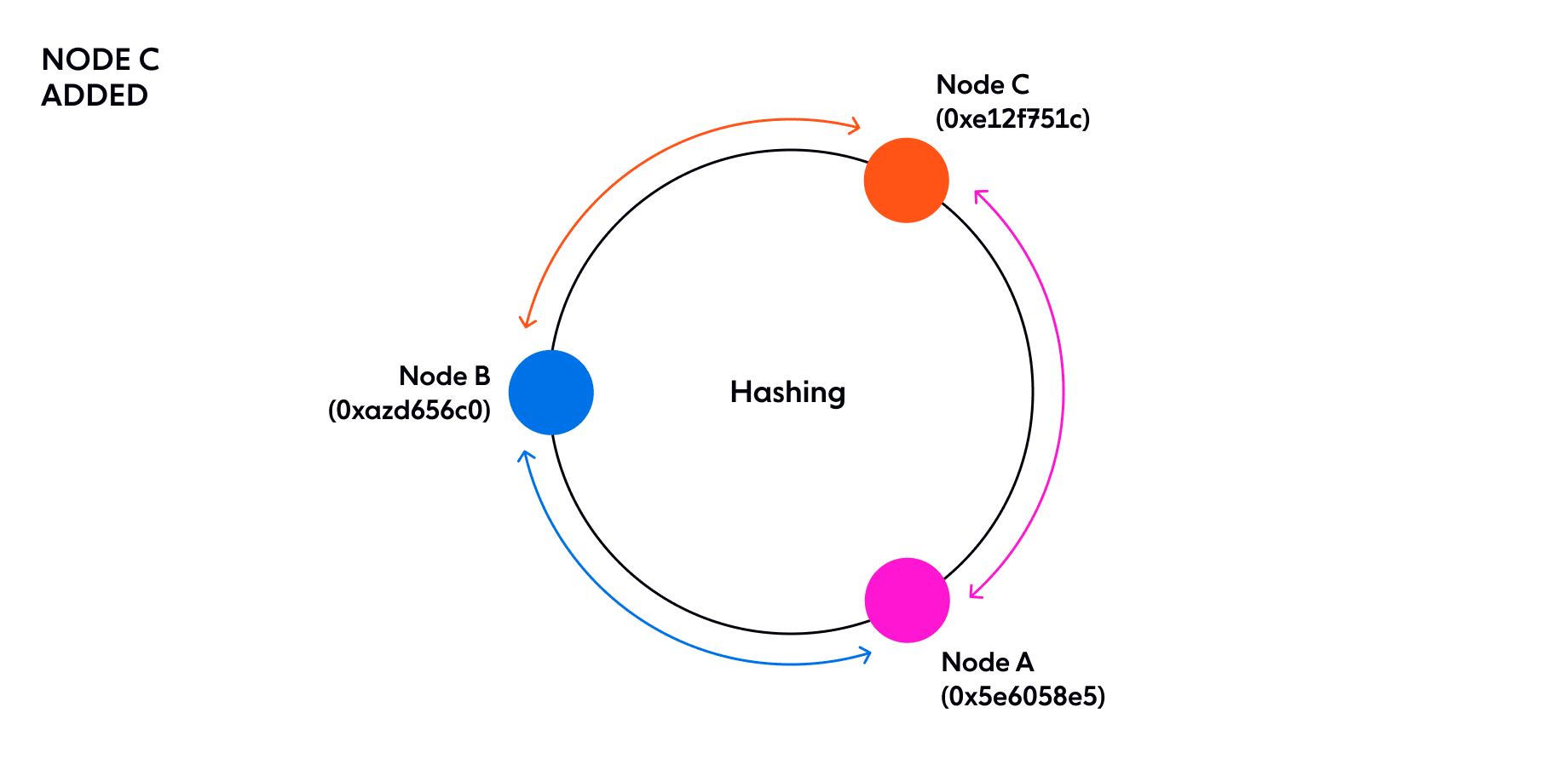
Suppose that now we add a new node to the ring called C. We generate a random hash for C.

• A: 0x5e6058e5
• B: 0xa2d65c0
• C: 0xe12f751c

Now, the ring space between 0xa2d65c0 + 1 and 0xe12f751c (which used to hash to A) are now delegated to C. All the other requests will continue to hash to the same node as before. To handle this shift of power, all the requests in that range that already exist on A will need to move all their state over to C.

You now understand why hashing is needed in distributed systems to distribute load evenly. Consistent hashing is required to minimize the amount of work needed in the cluster whenever there is a ring change.

Additionally, nodes need to exist at multiple locations on the ring to ensure statistically the load is more likely to be distributed more evenly. Iterating an entire hash ring for each ring change is inefficient. As your distributed system scales, having a more efficient way to determine what’s changed is necessary to minimize the performance impact of ring changes as much as possible. New index and data types are needed to solve this.

Consistent hashing FAQs

Where is consistent hashing used?

Here at Ably, we use consistent hashing within our distributed pub/sub messaging system to balance channels across all the available resources as uniformly as possible. Consistent hashing is also used for partitioning in Amazon's Dynamo storage system, by the Riak key-value database, and as part of the Akamai Content Delivery Network.

Why is it called “consistent”?

It is named as such because when a server is added or removed, it there is no need for the entire hash table to recalculated

What are pros and cons of various consistent hashing algorithms?

Of the various consistent hashing algorithms in common use, there are none that are perfect because of a need to balance factors such as distribution, memory usage and the time needed to do lookup, or to add/remove nodes.

Further reading from Ably Engineering

• Engineering dependability and fault tolerance in a distributed system
• Channel global decoupling for region discovery
• Stretching a point: the economics of elastic infrastructure

If you don’t know much about us, Ably provides cloud infrastructure and APIs to help developers simplify complex realtime engineering. We make it easy to power and scale live and collaborative features in apps, or distribute data streams to third-party developers as realtime APIs. Developers from startups to industrial giants build on Ably to simplify engineering, minimize DevOps overhead, and increase development velocity.

Try our APIs for free or get in touch.

Note: This article was first published June 2018. Updated July 2022